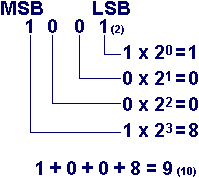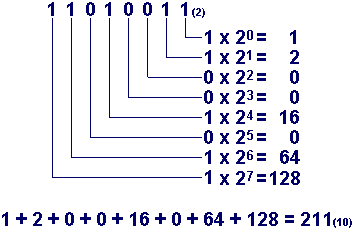Duale Zahlen (Binärzahlen)
Navigation
Allgemeines
Eine duale Zahl, auch binäre Zahl genannt, wird aus einer endlichen Kombination von Bits dargestellt. Durch eine Aneinanderreihung von Bits kann jede Information dargestellt werden.
verwendete Zeichen / Ziffern: 0 ;1
Im Dualsystem werden die Ziffern 0 und 1 und als Stellenwerte
die Potenzen zur Basis 2 benutzt. Die Wertigkeit jeder Stelle ergibt sich aus der Potenzierung der Basis 2 mit dem Stellenwert.
Stellenwerte:
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
2n |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
Rechenbeispiel
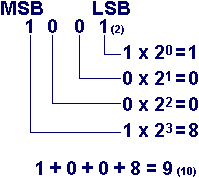
|
Das höchstwertigste Bit MSB
(most significant bit) steht am weitesten links, das niedrigstwertige
Bit LSB (least significant bit) steht am weitesten
rechts in einer Dual- bzw. Binärzahl. Die Wertigkeit der Bitfolge ergibt sich aus der Summe der einzelnden Wertigkeiten der Stellen. |
Schnelles Umwandlung von Dezimalzahlen in Dualzahlen
211 : 2 = |
105 Rest 1 |
LSB |
|
Wenn die Reste von MSB
zum LSB von links nach rechts notiert werden ergibt sich die Dualzahl.
211(10)= 1 1 0 1 0 0 1 1(2) |
105 : 2 = |
52 Rest 1 |
|
52 : 2 = |
26 Rest 0 |
|
26 : 2 = |
13 Rest 0 |
|
13 : 2 = |
6 Rest 1 |
|
6 : 2 = |
3 Rest 0 |
|
3 : 2 = |
1 Rest 1 |
|
1 : 2 = |
0 Rest 1 |
MSB |
siehe auch: Umwandlungen in Binär,
Oktal, Dezimal
und Hexadezimal
Lesen von Dualzahlen
Eine Dualzahl hat immer eine vorgeschriebene Bitlänge. So auch in unserem
Beispiel, nämlich 8 Bit. Schauen wir uns nun einmal an diesem Beispiel das Lesen
von Dualzahlen an.
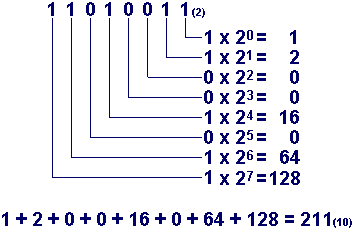
Darstellung negativer Zahlen
Die zusammengehörige Länge einer
Bitfolge bestimmt wie viele Ganzzahlen mit ihr dargestellt werden können.
Liegt eine Binärwortlänge von 8 Bit vor, so können Zahlen im
Bereich von 0 bis 255 mit ihr codiert werden. Ist es jedoch erwünscht,
dass auch negative Zahlen gespeichert werden, so muss dieses Intervall halbiert
werden. Bei einem vorliegenden 8-Bit-Wort ist das höchstwertige Bit 0,
bei negativen Zahlen ist das höchstwertige Bit 1. Die Zahlen im Intervall
0 bis 127 bilden wie gewohnt die positiven Zahlen. So wäre die Bitfolge
der 127 ganz gewohnt 01111111. Das linkeste Bit entscheidet, ob die vorliegende
Zahl positiv (Bit = 0) oder negativ (Bit = 1)
ist. Der Bereich der negativen Ganzzahlen erstrecht sich in einem 8-Bit-Wort
von -1 bis -128. Für die -1 lautet demnach die binäre Reihe 11111111.
Die 0 und die -128 sind nicht eindeutig codiert, da ihre Binärfolge das
Aussehen 00000000 aufweist. Deshalb wird meist bei Programmiersprachen ein der Definitionsbereich eines ganzzahligen Datentyps, der sowohl positive als auch negative Werte annehmen kann, definiert durch -2(Byteanzahl * 8 - 1) - 1 bis 2(Byteanzahl * 8 - 1).
Eine Umwandlung von positiven in negative Zahlen ist mit Hilfe des Einer- bzw. Zweierkomplement realisierbar.